Abstract: In the context of the three-phase hysteresis model (3PHL), a system of equations is established for a generalized thermoelastic medium under the influence of a magnetic field and an internal heat source. The problem is discussed using Eringen’s nonlocal elastic model. The exact expression of the physical quantity is obtained by normal mode analysis and illustrated graphically by comparison and discussion. All calculation results obtained are graphically presented and explained. This paper investigates a specific type of material called a generalized magneto-thermoelastic medium. This

A 2D first order linear system of partial differential equations of plane strain thermoelasticity within the frame of extended thermodynamics is presented and analyzed. The system is composed of the equations of classical thermoelasticity in which displacements are replaced with velocities, complemented with Cattaneo evolution equation for heat flux. For a particular choice of the characteristic quantities and for positive thermal conductivity, it is shown that this system may be cast in a form that is symmetric t-hyperbolic without further recurrence to entropy principle. While hyperbolicity

[No abstract available]

[No abstract available]

The study of nonlinear systems and chaos is of great importance to science and engineering mainly because real systems are inherently nonlinear and linearization is only valid near the operating point. The interest in chaos was increased when Lorenz accidentally discovered the sensitivity to initial condition during his simulation work on weather prediction. When a nonlinear system is exhibiting deterministic chaos, it is very difficult to predict its response under external disturbances. This behavior is a double-edged weapon. From a control and synchronization point of view, this proposes a

Mathematical Techniques of Fractional Order Systems illustrates advances in linear and nonlinear fractional-order systems relating to many interdisciplinary applications, including biomedical, control, circuits, electromagnetics and security. The book covers the mathematical background and literature survey of fractional-order calculus and generalized fractional-order circuit theorems from different perspectives in design, analysis and realizations, nonlinear fractional-order circuits and systems, the fractional-order memristive circuits and systems in design, analysis, emulators, simulation

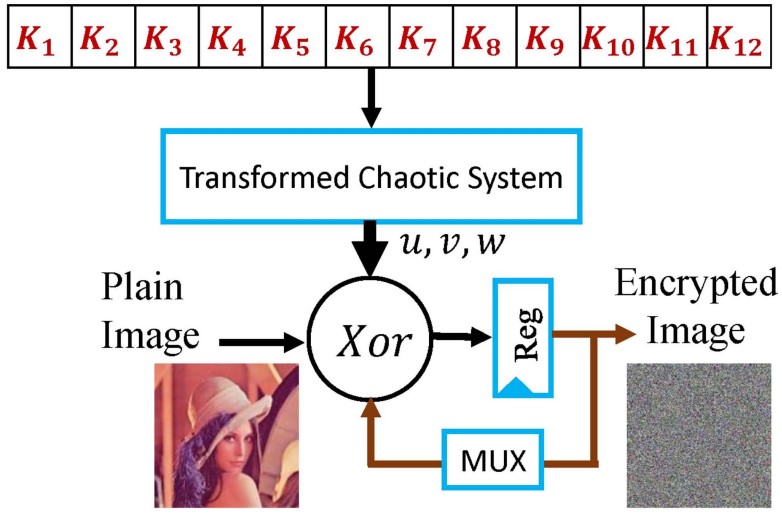
This article proposes a unified approach for hidden attractors control in fractional-order chaotic systems. Hidden attractors have small basins of attractions and are very sensitive to initial conditions and parameters. That is, they can be easily drifted from chaotic behavior into another type of dynamics, which is not suitable for encryption applications that require quite wide initial conditions and parameters ranges for encryption key design. Hence, a systematic coordinate affine transformation framework is utilized to construct transformed systems with self-reproducing attractors

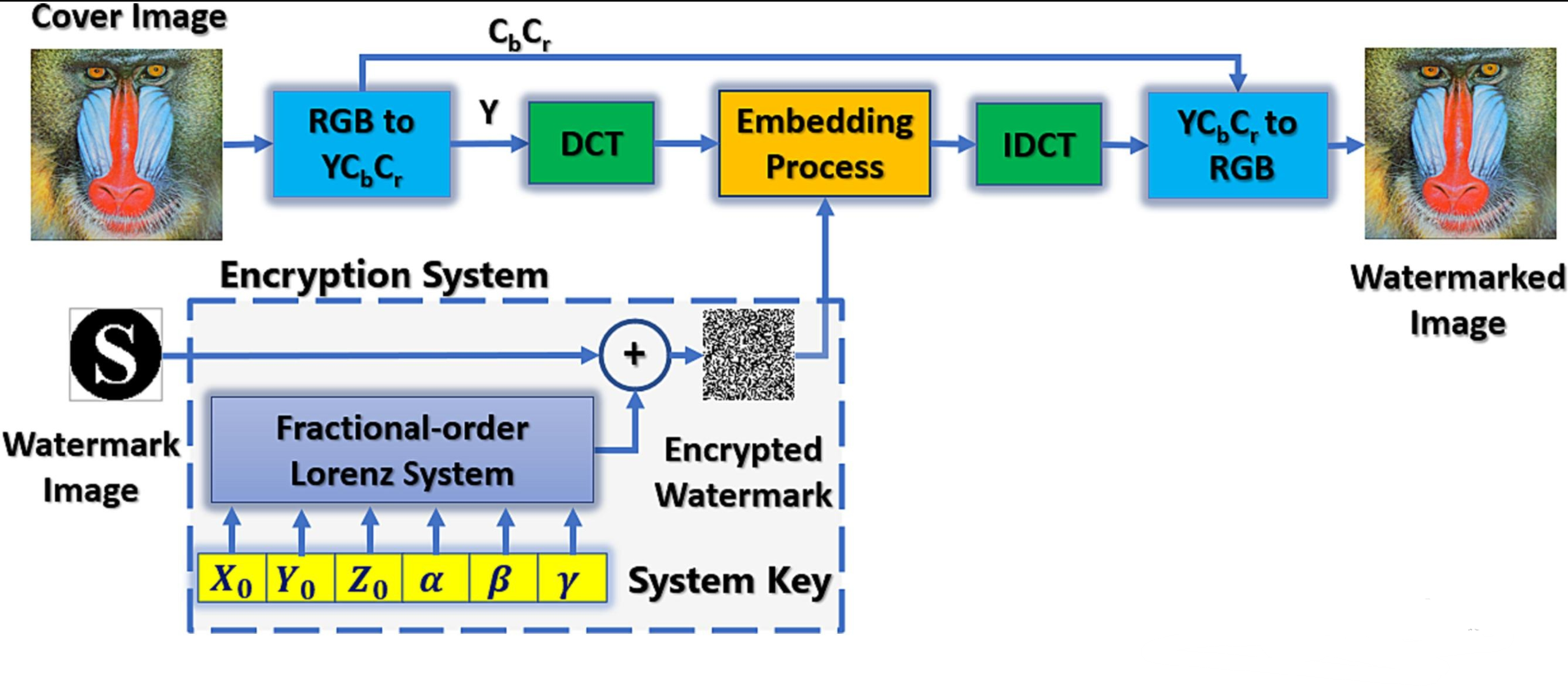
This paper investigates two different blind watermarking systems in the frequency domain with the development of a Pseudo Random Number Generator (PRNG), based on a fractional-order chaotic system, for watermark encryption. The methodology is based on converting the cover image to the YCbCr color domain and applying two different techniques of frequency transforms, Discrete Cosine Transform (DCT) and Discrete Wavelet Transform (DWT), to the Y channel. Then, the encrypted watermark is embedded in the middle-frequency band and HH band coefficients for the DCT and DWT, respectively. For more

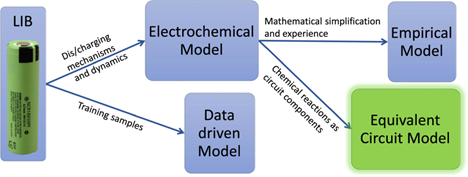
The precise identification of electrical model parameters of Li-Ion batteries is essential for efficient usage and better prediction of the battery performance. In this work, the model identification performance of two metaheuristic optimization algorithms is compared. The algorithms in comparison are the Marine Predator Algorithm (MPA) and the Partial Reinforcement Optimizer (PRO) to find the optimal model parameter values. Three fractional-order (FO) electrical equivalent circuit models (ECMs) of Li-Ion batteries with different levels of complexity are used to fit the electrochemical

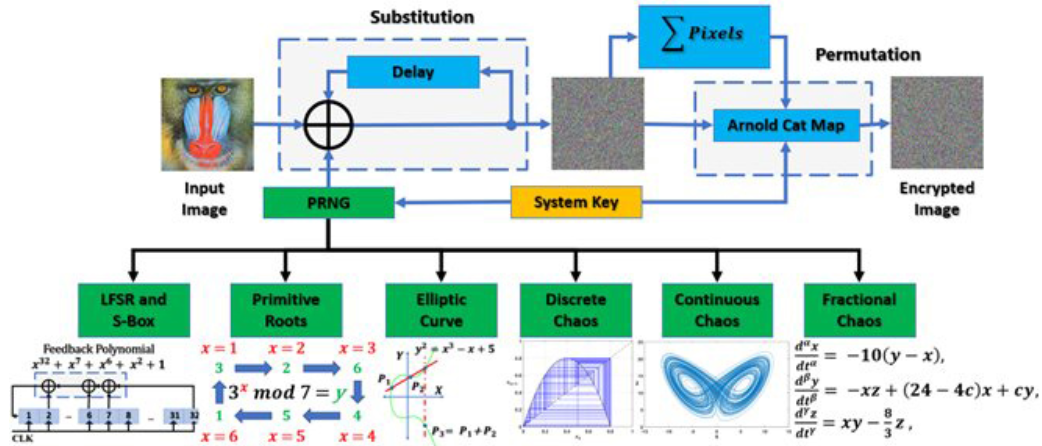
The design of an efficient Pseudo Random Number Generator (PRNG) with good randomness properties is an important research topic because it is a core component in many applications. Based on an extensive study of most PRNGs in the past few decades, this paper categorizes six distinct design scenarios under two primary groups: non-chaotic and chaotic generators. The non-chaotic group comprises Linear Feedback Shift Registers (LFSR) with S-Boxes, primitive roots, and elliptic curves, whereas the chaotic group encompasses discrete, continuous, and fractional-order chaotic generators. This paper