
Circuit Theory and Applications
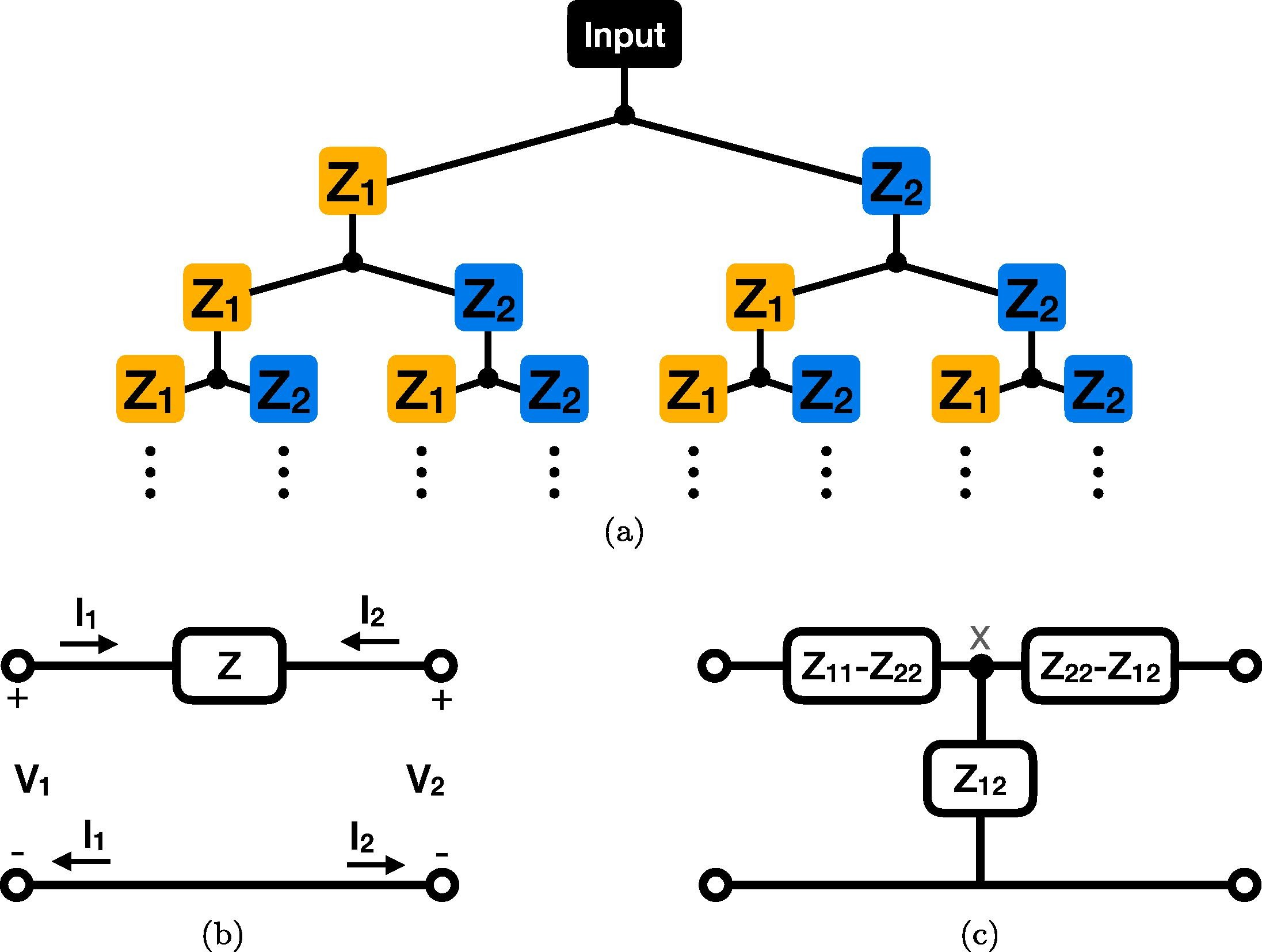
Generalizing the Warburg impedance to a Warburg impedance matrix
We seek to generalize and study the well-known Warburg impedance element, which has an impedance proportional to 1/s (s=jω is the complex frequency), to a two-port impedance network. For this purpose, we consider an infinite binary tree structure inside which each impedance is treated as a two-port network. We obtain a Warburg impedance matrix, which is both symmetrical and reciprocal, and study its equivalent circuit behavior. Interestingly, the equivalent circuit contains two resistors and a Cole–Davidson type impedance proportional to 1+2/(τs), where τ is a time constant. Simulation results

Synthesis of resonance-based common-gate fully differential band-pass filters
We propose a class of fully differential filters based on a common-gate differential amplifier cell in three different topologies. Our focus is on the synthesis of second-order band-pass filters and we found 53 possible circuits. All filters are resonance-based and have electronically tunable gain. Post layout simulations in 65-nm CMOS technology are provided to validate the proper function of these filters. © 2022 Elsevier B.V.
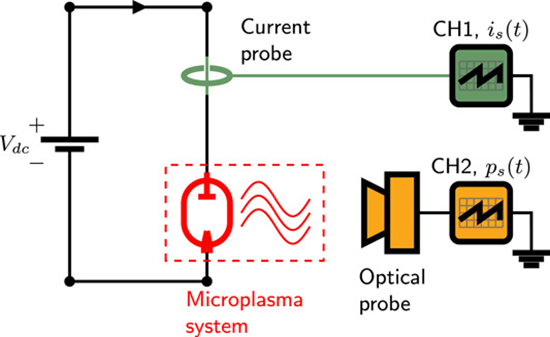
Parallel random bitstreams from a single source of entropy based on nonthermal electrochemical microplasma
This study presents the simultaneous generation of two uncorrelated and continuous high-quality random bitstreams originating from a single physical system based on confined, nonthermal electrochemical microplasma operating under atmospheric conditions. The randomness is intrinsically inherited from the time-resolved electrical current and optical emission intensities of the microplasma system, which were collected using wide bandwidth current probe and photodetection device. The parallel bitstreams pass unambiguously all 15 NIST SP 800-22 statistical tests without the need for any data post
A computational flow model of oxygen transport in the retinal network
The retina's high oxygen demands and the retinal vasculature's relatively sparse nature are assumed to contribute to the retina's specific vulnerability to vascular diseases. This study has been designed to model the oxygen transport in physiologically realistic retinal networks. A computational fluid dynamics study has been conducted to investigate the effect of topological changes on the oxygen partial pressure distribution in retinal blood vessels. The Navier Stokes equations for blood flow and the mass transport equation for oxygen have been coupled and solved simultaneously for the
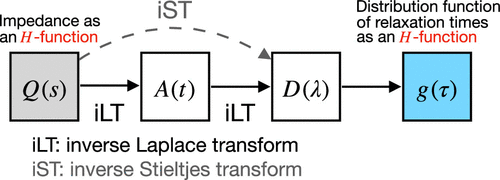
Procedure for Obtaining the Analytical Distribution Function of Relaxation Times for the Analysis of Impedance Spectra Using the Fox H-Function
The interpretation of electrochemical impedance spectroscopy data by fitting them to equivalent circuit models has been a standard method of analysis in electrochemistry. However, the inversion of the data from the frequency domain to a distribution function of relaxation times (DFRT) has gained considerable attention for impedance data analysis as it can reveal more detailed information about the underlying electrochemical processes without requiring a priori knowledge. The primary purpose of this paper is to provide a general and practical procedure for obtaining analytically the DFRT from

Fractional-order inverse filters revisited: Equivalence with fractional-order controllers
The equivalence of fractional-order inverse filters with fractional-order controllers is demonstrated in this work. This is achieved by appropriately rewriting the filters transfer functions in order to clarify the correspondence between the gain and time-constant of the filters and the scaling factor and differentiation/integration constant of the controllers. Possible implementations of fractional-order inverse filters using second generation voltage conveyors are presented and an application example, related to the control of a motion system, is demonstrated for evaluating the behavior of

Tikhonov regularization for the deconvolution of capacitance from the voltage–charge response of electrochemical capacitors
The capacitance of capacitive energy storage devices cannot be directly measured, but can be estimated from the applied input and measured output signals expressed in the time or frequency domains. Here the time-domain voltage–charge relationship of non-ideal electrochemical capacitors is treated as an ill-conditioned convolution integral equation where the unknown capacitance kernel function is to be found. This comes from assuming a priori that in the frequency domain the charge is equal to the product of capacitance by voltage, which is in line with the definition of electrical impedance
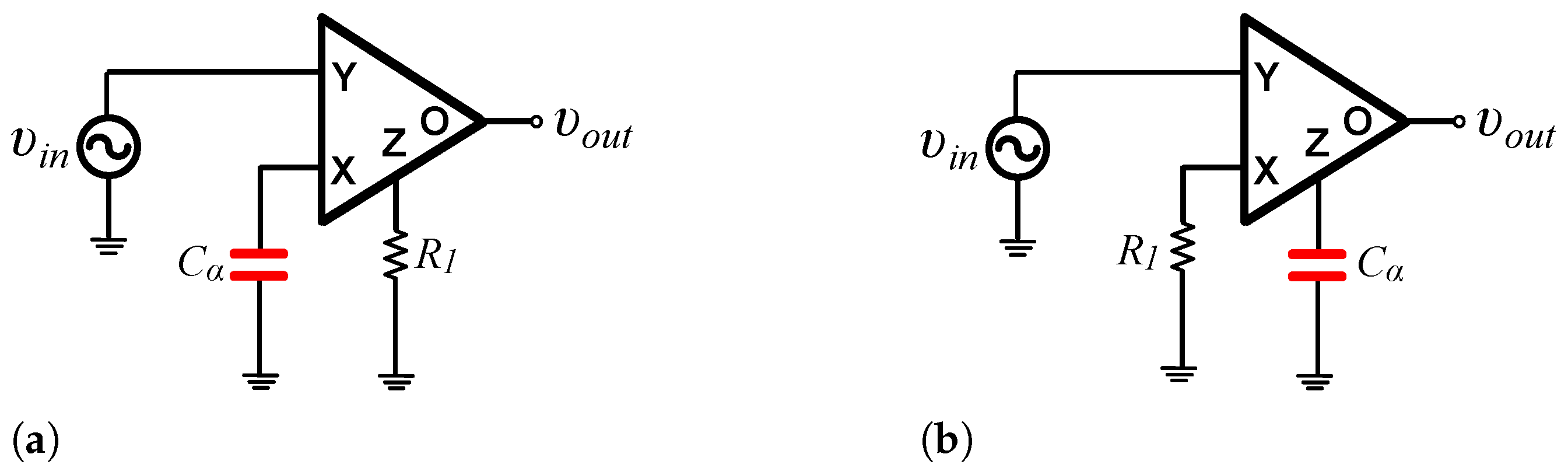
Implementation and Experimental Verification of Resistorless Fractional-Order Basic Filters
Novel structures of fractional-order differentiation and integration stages are presented in this work, where passive resistors are not required for their implementation. This has been achieved by considering the inherent resistive behavior of fractional-order capacitors. The implementation of the presented stages is performed using a current feedback operational amplifier as active element and fractional-order capacitors based on multi-walled carbon nano-tubes. Basic filter and controller stages are realized using the introduced fundamental blocks, and their behavior is evaluated through

Approximation and realization of power-law all-pass filters
Non-integer power-law all-pass transfer functions, are approximated by suitable integer-order transfer functions in this work. The derivation of the integer-order transfer functions is based on the analytic expansion of the (non-integer) power-law transfer functions through the utilization of the binomial theorem. The offered benefit is the derivation of stable integer-order transfer functions. This study is supported by experimental results, obtained using a Field Programmable Analog Array device, after the employment of curve fitting based approximation techniques. © 2022 Elsevier GmbH
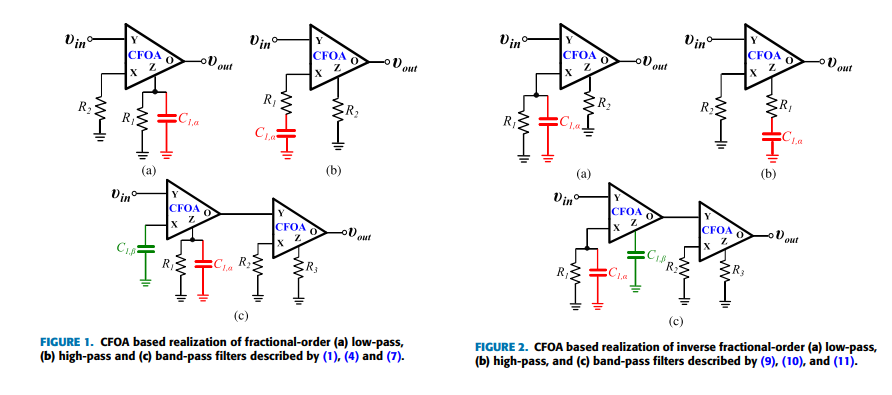
Non-Integer Order Generalized Filters Designs
Non-integer order filters can be derived from a generalized structure presented in this work. More specifically, fractional-order and power-law filters of single- or double-order are special cases of non-integer order filters with three degrees of freedom and can be implemented using a Current Feedback Operational Amplifier as the active element. The transfer function is formed as a ratio of two impedances which can be synthesized using Foster or Cauer RC networks. A curve-fitting based technique is employed for approximating the magnitude and phase of each impedance. The behavior of the