Generalizing the Warburg impedance to a Warburg impedance matrix

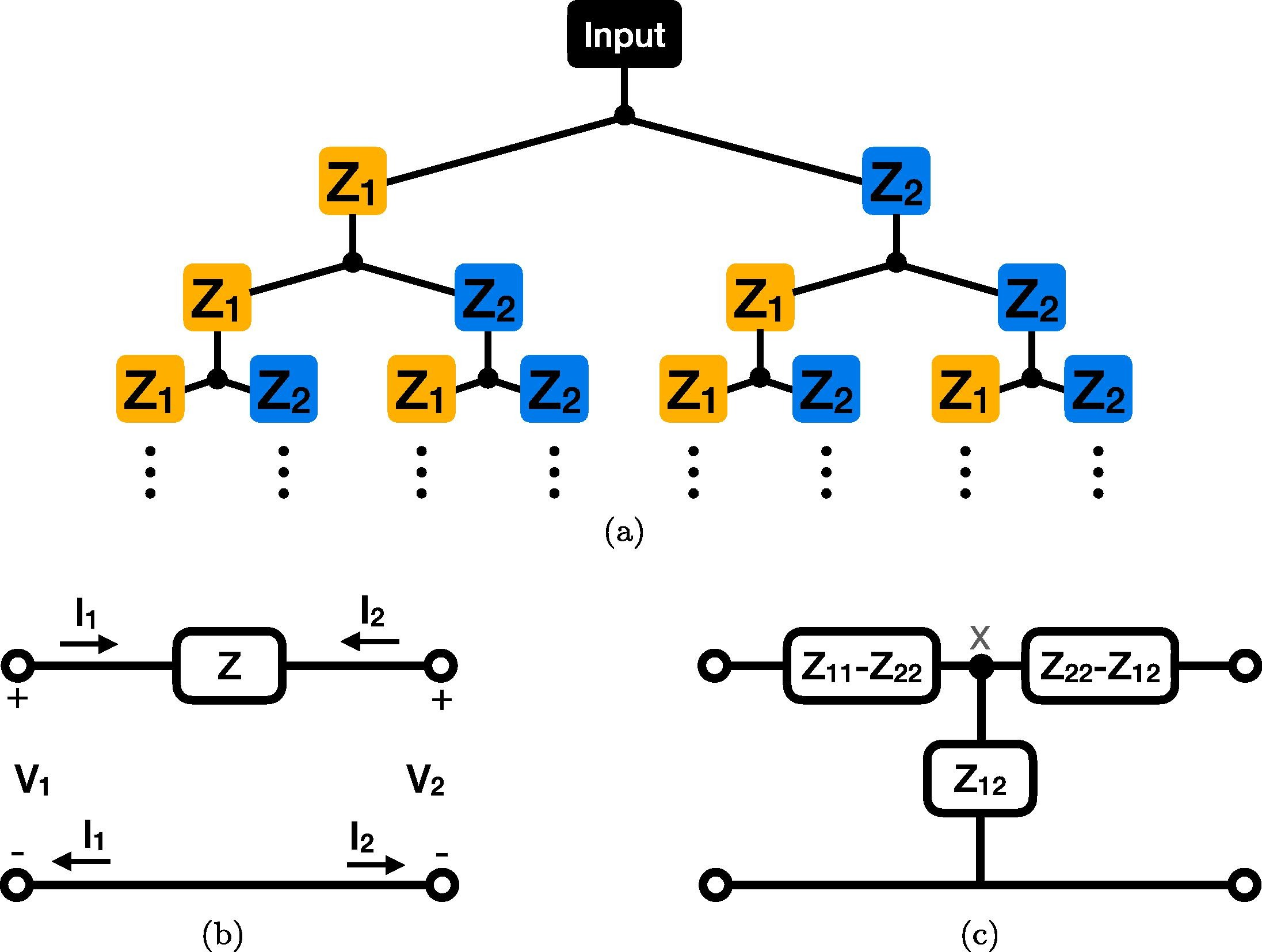
We seek to generalize and study the well-known Warburg impedance element, which has an impedance proportional to 1/s (s=jω is the complex frequency), to a two-port impedance network. For this purpose, we consider an infinite binary tree structure inside which each impedance is treated as a two-port network. We obtain a Warburg impedance matrix, which is both symmetrical and reciprocal, and study its equivalent circuit behavior. Interestingly, the equivalent circuit contains two resistors and a Cole–Davidson type impedance proportional to 1+2/(τs), where τ is a time constant. Simulation results of the Warburg impedance matrix and its implementation in a resonance circuit are provided and discussed. © 2022 Elsevier GmbH