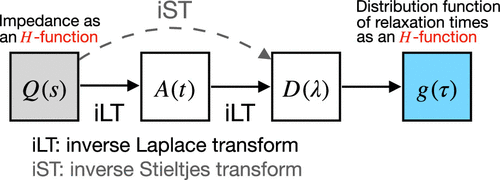
Procedure for Obtaining the Analytical Distribution Function of Relaxation Times for the Analysis of Impedance Spectra Using the Fox H-Function

The interpretation of electrochemical impedance spectroscopy data by fitting them to equivalent circuit models has been a standard method of analysis in electrochemistry. However, the inversion of the data from the frequency domain to a distribution function of relaxation times (DFRT) has gained considerable attention for impedance data analysis as it can reveal more detailed information about the underlying electrochemical processes without requiring a priori knowledge. The primary purpose of this paper is to provide a general and practical procedure for obtaining analytically the DFRT from an impedance model, assuming an elemental Debye relaxation model as the kernel. The obtained distributions, together with the usual practice of equivalent circuit modeling, can be used for the analysis of frequency-domain data, while serving as the benchmark for the existing numerical schemes. The procedure consists of first representing the impedance function in terms of the Fox H-function, which possesses many useful properties particularly that its Laplace transform is again an H-function. From there, the DFRT is obtained by two successive iterations of inverse Laplace transforms. In the passage, one can easily obtain an expression for the response function to a step excitation. The procedure is tested and verified on some known impedance models. © 2024 American Chemical Society.